|
|
 发表于 2024-1-9 17:13:13
|
显示全部楼层
发表于 2024-1-9 17:13:13
|
显示全部楼层
1# gracias
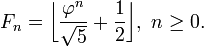

wayne 发表于 2012-2-20 13:47 [url=http://bbs.emath.ac.cn/redirect.php?goto=findpost&pid=41738&ptid=4054][/url]
${(F_{n+1}=F_n+F_{n-1}),(F_n=F_n):}$
所以得到
$[(F_{n+1}),(F_n)]=[(1,1),(1,0)][(F_n),(F_{n-1})]$
所以
$[(F_{n+1}),(F_n)]=[(1,1),(1,0)]^{n-1}[(F_2),(F_1)]=[(1,1),(1,0)]^{n-1}[(1),(1)]$ |
本帖子中包含更多资源
您需要 登录 才可以下载或查看,没有帐号?立即注册
x
|