|
|
 发表于 2024-4-10 16:40:01
|
显示全部楼层
发表于 2024-4-10 16:40:01
|
显示全部楼层
将模型定义为:
\(\begin{matrix}y(n)=c+a\exp(kx)\cos(px+q),&x=n-805\end{matrix}\)
数据文件 Data.txt 中第一列数据对应变量 \(n\) ,第二列数据对应变量 \(A(n)\) 。
取中间 \(806\le n\le2418\) 一段数据建模:
自变量:\(x=1,2,\dots,1613\)
应变量:\(y_0=A(806),A(807),\dots,A(2418)\)
取数据文件 Data.txt 中最后一行的数据 \(A(11975)\) 作为模型参数 \(c\) 的初始值。
即取:\(c = 0.9989539604497421125056471767972029556836\) 。
减去常数项,并取绝对值和对数,即:\(y_1=\log|y_0-c|\) 。
拟合线性模型:\(y_1=kx+\beta\) 得 \(k=-0.0100399257488,\beta=51.708275431\) ,
取 \(k\) 的初始值 \(k=-0.0100399257488\) 。
再去除指数分量:\(y_2=10^{23}(y_0-c)\exp(-kx)\) 。
注:常数 \(10^{23}\) 将数据放大,以方便模型拟合计算。
拟合正弦模型:\(y_2=a\sin(px+q)\) 得 \(a=6.986,p=0.2509,q=1.701\),
取 \(a,p,q\) 的初始值 \(a=6.986\times10^{-23},p=0.2509,q=1.701\) 。
至此得到模型参数的初始值:
\(c = 0.99895396044974211250564717679720295568360\)
\(a=6.986\times10^{-23}\)
\(k=-0.0100399257488\)
\(p=0.2509\)
\(q=1.701\)
从模型的初始参数出发,通过优化模型参数,使得模型残差最小。
模型残差的衡量指标为两个正弦分量的均方差 (MSE - Mean Squared Error) :
\(MSE=\frac{1}{N}\sum_{i=1}^N[y_{observed}(i)-y_{predicted}(i)]^2\)
下图为初始模型参数下得到的残差图:
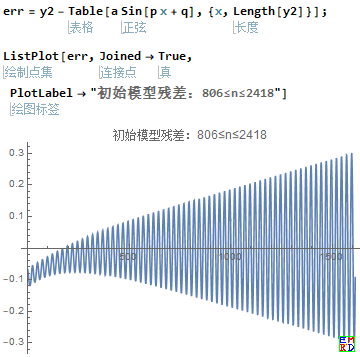
这个图说明模型参数有待优化。 |
本帖子中包含更多资源
您需要 登录 才可以下载或查看,没有帐号?立即注册
x
|